1. Altura del jardín de Franchy en relación a la casa de Cólogan

Empecemos por calcular la altura h1.

Nos situamos en la casa de Cólogan y miramos hacia el jardín de Franchy. ¿A qué altura, h1, está?

Si trazamos el triángulo rectángulo de la figura 4, podemos calcular la altura con el ángulo de elevación desde A y la hipotenusa AD.

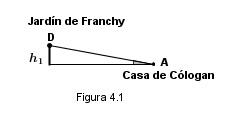
El ángulo de elevación en A lo obtiene Borda midiendo con los instrumentos de que disponía. Pero ¿cómo medir la distancia AD?

Medida de la distancia AD

Desde la casa de Cólogan (A) hasta el jardín de Franchy (D) el terreno es bastante irregular y demasiado largo. No podemos medir la distancia experimentalmente. Acudimos, entonces, a las triangulaciones ya comentadas.

Para calcular la hipotenusa AD de la figura 4.1, Borda toma el punto C, la montañeta del Puerto, y traza el triángulo ADC, con base AC. Es un triángulo sobre el terreno, de vértices accesibles y visibles. Puede medir sus ángulos. Sin embargo, la base sigue siendo demasiado grande para obtenerla empíricamente.

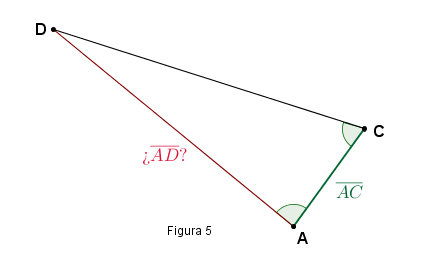
Borda vuelve a triangular eligiendo un punto B, cerca del Jardín Botánico y trazando el triángulo ABC con base AB (ver ilustración 4)[2].

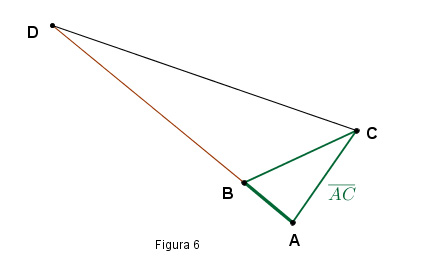
En éste sí mide los aproximadamente 447 metros de la base (AB), con las pértigas de 15 pies. De hecho, es la única medida longitudinal real que hace; las demás las obtiene mediante cálculos matemáticos.

“Nuestra base fue medida por dos diferentes secciones de operadores: la primera halló 1.377 pies seis pulgadas; la segunda, 1.377 pies tres pulgadas seis líneas” (ver ilustración 3)

Las relaciones trigonométricas le permiten obtener la longitud AC, después de determinar la amplitud de los ángulos con los círculos.

En el triángulo ADC, con la longitud AC y las medidas de los ángulos, calcula la longitud AD, de 8.647pies 3 pulgadas (aproximadamente 2.808 metros).

Por fin, en la figura 4.1, ya se tiene la hipotenusa AD. Con ésta y el ángulo de elevación desde A, la altura h1 que obtiene nuestro geómetra es 733 pies 6 pulgadas (aproximadamente 238 metros).

[2] Los puntos a, b y d están a distinta altitud y entre los ángulos CAD y CAB hay una diferencia de 4’ 45’’. Sin embargo, hemos optado por dibujarlos en el mismo segmento para que coincida con la ilustración de Humboldt reproducida en el módulo “Medición histórica del Teide”. El dibujo de Humboldt (ilustración 5) aparece en ‘Voyage aux régions equinocciales du Nouveau Continent. Tome Premier’ de Aimé Bonpland y Alexander von Humboldt, 1814.