3. Altura de la casa de Cólogan respecto del nivel del mar

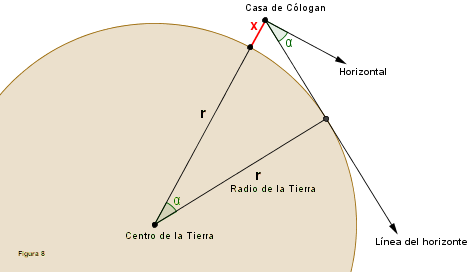Por último, es necesaria la elevación de la casa de Cólogan (punto A) respecto del nivel del mar. Esto lo hace Borda midiendo los ángulos de depresión del horizonte en la casa de Cólogan y en el jardín de Franchy.

En la figura 8, si x es la altura a calcular y α el ángulo de depresión medido, el coseno de α proporciona una ecuación en x y r (radio de la Tierra):

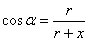
Borda no usa el radio de la Tierra sino que busca otra ecuación similar, tomando el ángulo de depresión desde el jardín de Franchy. Obtiene así que x es 283,6 pies (altura de la casa de Cólogan sobre el nivel del mar).

Por tanto,

Altura del Teide = 11.146,3 + 283,6 ≈ 11.430 pies ≈ 1.905 toesas ≈ 3.713 metros