Medición de la altura del Teide de Jean Charles Borda

Jean Charles Borda, miembro de la Academia de las Ciencias de París, viene a Canarias dos veces y en ambas ocasiones realiza mediciones del Teide. La primera, en 1771, resulta infructuosa ya que, de vuelta a Francia, se da cuenta de un error en la toma de datos. Su espíritu científico le hace poner todo su empeño para volver y lo consigue en 1776. Esta segunda expedición se organiza para verificar la precisión de ciertos cronómetros (necesarios para conocer la longitud en las travesías marinas), medir el Teide y cartografiar las Islas y la costa africana próxima. Dedicaremos las siguientes páginas a la medición trigonométrica que hizo en este viaje.

Las matemáticas en los cálculos de Borda

¿Cómo medir la altura de una montaña?

Matemáticamente se puede calcular la altura (h) de un punto (P) construyendo un triángulo rectángulo (ver figura 1). Si en este triángulo se conocen dos elementos independientes, se puede resolver el triángulo. Por ejemplo, sabiendo el ángulo de elevación de P en relación a A y la distancia

AP, se obtiene la altura h, sin más que aplicar la definición de seno de un ángulo (fórmula ).

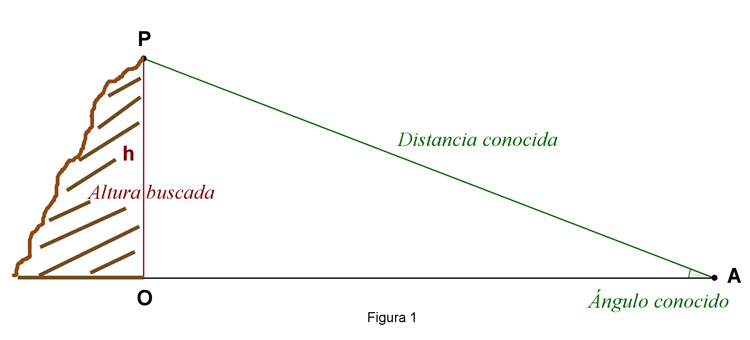
Este planteamiento tan sencillo, de figuras ideales, se complica mucho cuando lo trasladamos a la realidad. En el caso de la altura del Teide, medir el ángulo de elevación en cualquier punto (A) desde el que se divisase el Pico, era posible con los instrumentos de medida de ángulos, bastante precisos, traídos por Borda. El problema estaba en la distancia desde el punto elegido hasta el Pico (distancia AP) ya que medir esta longitud experimentalmente era imposible.

Para salvar este tipo de dificultades, los científicos recurrían a las triangulaciones sobre el terreno. Si no se podía medir AP, se buscaba un punto auxiliar X, visible y accesible, tal que la distancia AX sí fuese medible de forma empírica. Entonces trazando el triángulo AXP y midiendo AX y dos de los ángulos del triángulo, las relaciones trigonométricas les daban la longitud AP.

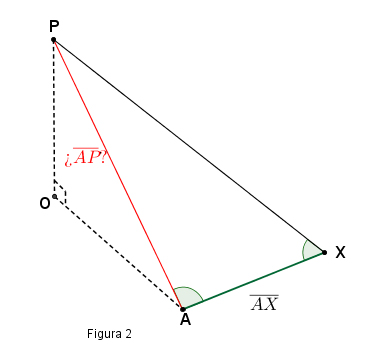
¿Cómo adaptó Borda estos conocimientos a su medición de la altura del Teide?

La idea inicial pudo haber sido trazar un triángulo rectángulo como el de la figura 1, con vértice P, el pico del Teide y vértice A, un punto al nivel del mar, en la costa (ver ilustración 1). Para obtener la hipotenusa AP, se buscaría otro triángulo sobre el terreno, eligiendo el punto X convenientemente (ver figura 2). Pero, como él mismo escribe:

“Siendo desigual y cortado por quiebras el terreno en torno del Puerto de la Orotava, no nos fue posible encontrar allí una base bastante grande para determinar la distancia del Pico mediante un solo triángulo…”

Efectivamente, para obtener una distancia como AP, se necesita un triángulo auxiliar de base AX lo suficientemente grande como para no acumular demasiados errores en los cálculos.

Borda, en lugar de un solo triángulo AOP, utiliza dos triángulos para calcular la altura, y tres para las hipotenusas de esos dos triángulos. Así consigue minimizar los errores de las medidas. Para los ángulos emplea el cuarto de círculo de Ramsden y el círculo de reflexión que lleva su nombre. La medición longitudinal la efectúa con tres pértigas de 15 pies (4,87 m aproximadamente) de largo cada una. Obtiene 3.713 m para la altura del Teide. Hoy, mediante el GPS, se estima la altura en 3.716 m.